DESKRIPSI HEWAN
1. HAMSTER
binatang sejenis hewan pengerat, terdapat berbagai jenis di dunia dan
hampir ada di tiap negara. termasuk ke dalam subfamili cricetinae.
Subfamili ini terbagi ke dalam sekitar 18 spesies, yang diklasifikasikan
ke dalam enam atau tujuh genus.
Memiliki badan yang gemuk, dengan
ekor yang lebih pendek daripada badannya dan memiliki telinga yang
berbulu, kaki yang lebar, pendek dan pendek gemuk. memiliki bulu yang
tebal dan panjang, dan bulunya memiliki berbagai warna tergantung
spesiesnya, contohnya hitam, abu-abu, putih, coklat, kuning dan merah.
Bagian bawah berwarna putih sampai abu-abu dan hitam..
Habitat nya di utara terletak dari Eropa tengah sampai Siberia,
Mongolia, dan Tiongkok utara sampai Korea. Mereka hidup di perbatasan
padang pasir, bukit pasir yang divegetasi, bukit di kaki gunung dan
dataran rendah yang bersemak-semak dan berbatu, sungai di lembah, dan
padang rumput yang luas, beberapa juga tinggal di ladang tanam. Sebaran
geografi menggambarkan kelompok spesies.
Termasuk makhluk omnivora.
Makanan mereka biasanya butir padi, tetapi juga termasuk buah segar,
akar, bagian hijau tumbuhan, invertebrata dan beberapa binatang kecil
lainnya (serangga seperti belalang).membawa makanan mereka di pipi
dimana di dalamnya terdapat kantung untuk dimasukan kedalam lubang
makanan mereka.Namun, tidak
semua makanan cocok untuk nyar, beberapa makanan, seperti daun beracun
dari tomat, menjadi makanan yang paling berbahaya untuk kesehatan.
Kelakuannya biasanya bersifat diam dan nokturnal walaupun juga dapat
dikatakan krepuskular dan mereka terkadang aktif pada awal pagi hari
atau akhir sore. Mereka adalah penggali yang baik, membuat lubang dengan
pintu masuk satu atau lebih dan dengan galeri yang terhubung dengan
kamar mereka untuk sarang, gudang makanan dan aktivitas lainnya. Tidak
ada yang berhibernasi selama musim dingin, tetapi beberapa pengalaman
periode torpor terjadi selama beberapa hari sampai beberapa bulan.
2. GAJAH
Mempunyai belalai yang panjang , berwarna abu abu , mempunyai bentuk
tubuh yang besar, termasuk dalam golongan herbivora, kita dapat
menjumpai di kebun binatang atau hutan, salah satu ciri khasnya yaitu
memiliki gading , ia biasa mengambil makanannya dengan menggunakan
hidung atau belalainya, mereka hidup secara berkelompok,pada umumnya
banyak manusia yang memburunya hanya untuk mendapatkan gadingnya , ia
termasuk salah satu yang di lestarikan.
3. Tupai
Segolongan
mamalia kecil yang
mirip, dan kerap dikelirukan, dengan bajing. Secara ilmiah, hewan ini tidak sama dan jauh kekerabatannya dari
keluarga bajing. Hewan ini adalah pemangsa serangga dan dahulu
dimasukkan ke dalam bangsa pemakan serangga
bersama-sama dengan cerurut, sedangkan
bajing dan bajing terbang termasuk bangsa Rodentia (hewan pengerat)
bersama-sama dengan tikus.
Hewan
ini memiliki otak yang relatif
besar. Rasio besar otak berbanding besar tubuh pada hewan ini adalah yang
terbesar pada makhluk hidup, bahkan mengalahkan manusia. Namun menurut pendapat
terbaru berdasarkan kajian kekerabatan molekuler (molecular phylogeny),
kini digolongkan tersendiri ke dalam bangsa Scandentia; yang bersama-sama
dengan kubung (bangsa
Dermoptera) dan bangsa Primata di atas, menyusun kelompok hewan yang disebut
Euarchonta.
4. ANJING CIHUAHUA
Memiliki tubuh yang kompak dan agak sedikit panjang. Ekornya tidak
dipotong (undocked) dan tidak terlalu panjang. Ekornya biasanya
melengkung ke arah punggung (tea cup tail) , menunjuk ke arah kepala dan
tegak lurus seperti antena. Batok kepala berbentuk buah apel (apple
dome), Kalau dilihat dari samping, antara batok kepala dan moncong
meiliki sudut 90 derajat. Batok kepala harus berbentuk bulat jika
dilihat dari depan bukan kotak . biasanya memiliki molera (lubang) di
atas kepala pada saat lahir dan akan merapat atau hilang pada saat
dewasa. Warna mata harus berwarna gelap, hidung berwarna hitam atau
coklat jika warna bulunya putih atau warna muda. Kuping nya berdiri
tegak dan letaknya membentuk sudut 45 derajat jika dilihat dari depan.
tidak memiliki kuping seperti kuping Miniature Pincher yang posisinya
tegak lurus ke atas.
Memiliki 2 jenis bulu; bulu pendek (smooth coat) dan bulu panjang
(long coat) . Keduanya boleh saling dikawinkan tidak seperti anjing
Dachshund atau Fox Terrier yang tidak boleh dikawinkan jika type bulunya
berbeda. Kadang dari perkawinan antara bulu pendek dapat menghasilkan
bulu panjang begitu juga sebaliknya.. Berat badannya berkisar antara 1
Kg – 2,7 Kg dengan tinggi badan sampai 20 CM diukur sampai punggung.
5. Kucing
Hewan
ini termasuk mamalia, berkaki empat dan juga termasuk hewan vertebrata
(bertulang belakang). Hewan ini tidak
berbahaya, bahkan banyak dijadikan sebagai hewan peliharaan. Tetapi ada
satu-satunya bahaya yang disebabkan hewan ini adalah kemungkinan terjadinya
infeksi rabies akibat gigitannya dan juga cakaran dari kuku kucing yang sangat
perih dan menyakitkan.
Hewan
ini dapat berakibat fatal bagisuatu ekosistem yang bukan tempat tinggal
alaminya. Pada beberapa kasus, kucing dapat menyebabkan kepunahan. Kucing menyergap
dan melumpuhkan mangsa dengan cara yang mirip dengan singa dan harimau,
menggigit leher mangsa dengan gigi taring yang tajam sehingga melukai saraf
tulang belakang atau menyebabkan mangsa kehabisan napas dengan merusak
tenggorokan.
sumber :
http://uthyns.blogspot.com/2013/10/deskripsi-hewan-dan-tumbuhan_20.html
http://ranimonica.wordpress.com/2012/12/04/deskripsi-hewan/
http://sherlyyunitabahrun.wordpress.com/2013/01/13/deskripsi-tentang-hewan-dan-tumbuhan/







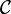





 atau
atau 


 ,
,  ,
,  ,
, 












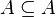



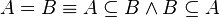

 adalah sebuah keluarga himpunan. Perhatikan bahwa untuk sembarang himpunan A, maka himpunan kuasanya,
adalah sebuah keluarga himpunan. Perhatikan bahwa untuk sembarang himpunan A, maka himpunan kuasanya,  bukanlah sebuah kelas, karena mengandung anggota c yang bukan himpunan.
bukanlah sebuah kelas, karena mengandung anggota c yang bukan himpunan.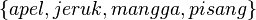 adalah 4. Himpunan
adalah 4. Himpunan  juga memiliki anggota sejumlah 4. Berarti kedua himpunan tersebut
ekivalen satu sama lain, atau dikatakan memiliki kardinalitas yang sama.
juga memiliki anggota sejumlah 4. Berarti kedua himpunan tersebut
ekivalen satu sama lain, atau dikatakan memiliki kardinalitas yang sama. yang memetakan satu-satu dan kepada himpunan A ke B, maka kedua himpunan tersebut memiliki kardinalitas yang sama.
yang memetakan satu-satu dan kepada himpunan A ke B, maka kedua himpunan tersebut memiliki kardinalitas yang sama. .
.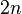 .
.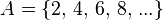
 . Pembuktian bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian diagonal.
. Pembuktian bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian diagonal. .
.
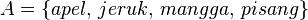 maka:
maka:


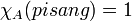

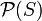 dengan himpunan dari semua fungsi karakteristik dari S.
Hal ini mengakibatkan kita dapat menuliskan himpunan sebagai barisan
bilangan 0 dan 1, yang menyatakan ada tidaknya sebuah anggota dalam
himpunan tersebut.
dengan himpunan dari semua fungsi karakteristik dari S.
Hal ini mengakibatkan kita dapat menuliskan himpunan sebagai barisan
bilangan 0 dan 1, yang menyatakan ada tidaknya sebuah anggota dalam
himpunan tersebut.